?全國2012年4月高等教育自學考試《高等數學(工本)》試題
摘要:本試卷總分100分,測試時間150分鐘。
點擊查看>>>全國自考00023高等數學(工本)專業歷年真題
本試卷總分100分,測試時間150分鐘。
一、單項選擇題(每小題3分,共15分)
1.下列曲面中,母線平行于y軸的柱面為( )
A.z = x^2
B.z = y^2
C.z = x^2 + y^2
D.x + y + z =1
2.已知函數h ( x, y ) = x – y + f ( x + y ),且h (0,y) = y^2,則f ( x + y )為( )
A.y (y + 1)
B.y (y - 1)
C.( x + y)( x + y -1)
D.( x + y )( x + y +1)
4.微分方程y![]() =x的階數是( )
=x的階數是( )
A.0
B.1
C.2
D.3
3.下列表達式是某函數u(x,y)的全微分的為( )
A.x^2ydx + xy^2dy
B.xdx + xydy
C.ydx - xdy
D.ydx + xdy
5.無窮級數![]() 的和為( )
的和為( )
A.e + 1
B.e - 1
C.e - 2
D.e + 2
一、填空題(本大題共5小題,每空2分,共10分)
1.已知向量a={-2,c,6}與向量b={1,4,-3}垂直,則常數c = ______。
2.函數![]() 的定義域為______。
的定義域為______。
3.二次積分 ,交換積分次序后
I=
______。
,交換積分次序后
I=
______。
4.已知![]() 的解,則常數
c= ______。
的解,則常數
c= ______。
5.冪級數![]() 的收斂半徑R
=______。
的收斂半徑R
=______。
三、計算題(每小題5分,共60分)
1.將直線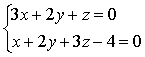 化為參數式和對稱式方程.
化為參數式和對稱式方程.
5.計算二重積分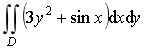 ,其中積分區域D是由y = | x |和y = 1所圍成.
,其中積分區域D是由y = | x |和y = 1所圍成.
6.計算三重積分I= ,其中積分區域Ω是由x^2+y^2=4及平面z = 0,z = 2所圍的在第一卦限內的區域.
,其中積分區域Ω是由x^2+y^2=4及平面z = 0,z = 2所圍的在第一卦限內的區域.
3.求曲面z = 2y + ln![]() 在點(1,1,2)處的切平面方程.
在點(1,1,2)處的切平面方程.
7.計算對弧長的曲線積分I=![]() ,其中L為圓周x^2+y^2=9的左半圓.
,其中L為圓周x^2+y^2=9的左半圓.
2.設方程f ( x + y + z, x, x + y)=0確定函數z = z ( x, y ),其中f為可微函數,求![]() 和
和![]() .
.
9.驗證y1 = e^x,y2 = x都是微分方程(1 – x)![]() +
+![]() -y = 0的解,并寫出該微分方程的通解。
-y = 0的解,并寫出該微分方程的通解。
4.求函數z = x^2 - y^2在點(2,3)處,沿從點A(2,3)到點B(3,3+![]() )的方向l的方向導數.
)的方向l的方向導數.
8.計算對坐標的曲線積分I=![]() ,其中L是平面區域
D:x2 + y2 ≤4的正向邊界.
,其中L是平面區域
D:x2 + y2 ≤4的正向邊界.
12.設函數f ( x )=x^2cosx的馬克勞林級數為 ,求系數a6.
,求系數a6.
11.設α為任意實數,判斷無窮級數![]()
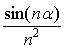 的斂散性,若收斂,是絕對收斂還是條件收斂?
的斂散性,若收斂,是絕對收斂還是條件收斂?
10.求微分方程x![]() 的通解.
的通解.
四、綜合題(每小題5分,共15分)
1.設函數z=ln(![]() +
+![]() ),證明2x
),證明2x![]() +2y
+2y![]() =1.
=1.
3.將函數f ( x )=![]() 展開為x的冪級數.
展開為x的冪級數.
2.求函數f ( x, y)=3+14y+32x-8xy-2y^2-10x^2的極值.
延伸閱讀
- 考前自救指南:希賽自考題庫快速提分
- 自考專屬刷題工具,刷題即提分!
- 最后9天,自考歷年真題應該怎么刷?
- 自考備考一站式服務:希賽自考題庫APP
- 0基礎逆襲秘籍:希賽全套自考學習包(含智能題庫)
- 避開備考誤區!用希賽自考APP快速提分!

自考微信公眾號

掃碼添加
自考備考資料免費領取
去領取











 掃描二維碼
掃描二維碼